[자바스크립트 자료구조] 힙(heap) - 연습문제
2021. 3. 25. 13:12ㆍFront-end/자료구조
728x90
반응형
일련의 숫자에서 중앙값 찾기
중앙값이란
어떤 배열을 정렬했을 때 정 가운데에 위치하는 값
원소의 개수가 홀수인 경우: 가장 중앙에 위치한 원소가 중앙 값((전체 개수 + 1) / 2 번째 원소)
- [1, 2, 3]의 배열에서는 2가 중앙값
원소의 개수가 짝수인 경우: 가운데 두 원소의 평균이 중앙값
- [1, 2, 3, 4]에서는 2와 3의 평균인 2.5가 중앙값
중앙값을 찾을 때 그냥 최소힙이나 최대힙 둘중 하나로 만들고 중앙에 해당하는 인덱스에 있는 값을 반환하면 되겠지만 데이터가 지속적으로 추가/삭제되고 있는 상황에서 중앙값을 찾으려면 중앙값을 찾을때마다 배열 전체에 대한 정렬을 시도하므로 시간 낭비임
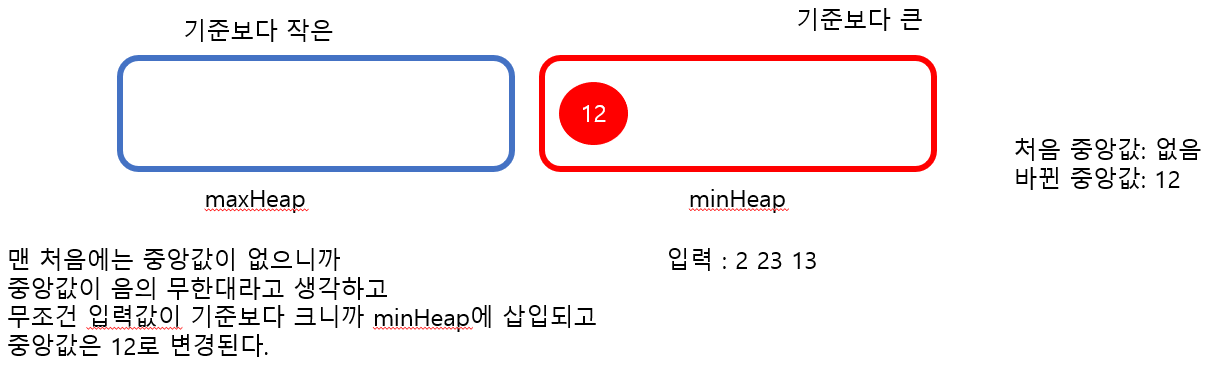
🌟🌟🌟하나의 최소 힙과 최대 힙을 만들면 중간 값을 얻는 것은 단지 O(1) 시간 밖에 걸리지 않음
그래서 중앙값을 위한 힙을 따로 정의하면 된다.
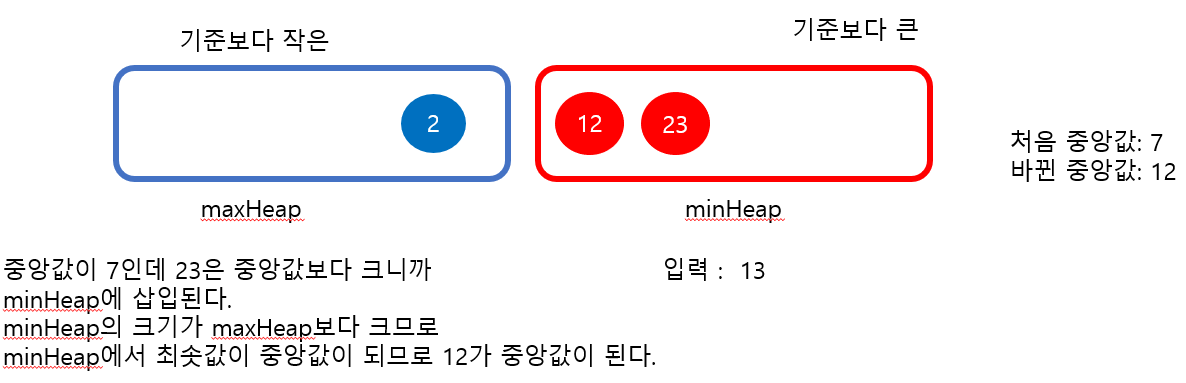
minHeap과 maxHeap을 따로 정의하고, 중앙값보다 크면 maxHeap에 저장하고 중앙값보다 작으면 minHeap에 저장한다. 그리고, Max heap과 Min heap의 크기가 균형되도록 조절한다. 다만, 기준을 고려해 기준을 가진쪽이 하나는 더 클 수 있도록 허용한다.



class MedianHeap{
constructor(){
this.minHeap = new MinHeap();
this.maxHeap = new MaxHeap();
this.count = 0;
}
add(value){
//중앙값 보다 작으면 maxheap에 삽입
//중앙값 보다 크면 minheap에 삽입
this.count++;
if(value > this.median()){
this.minHeap.add(value);
}else{
this.maxHeap.add(value);
}
if(this.minHeap.size() - this.maxHeap.size() > 1){
this.maxHeap.add(this.minHeap.poll());
}
if(this.maxHeap.size() - this.minHeap.size() > 1){
this.minHeap.add(this.maxHeap.poll());
}
}
median(){
if(this.minHeap.size() === 0 && this.maxHeap.size() === 0){
return Number.NEGATIVE_INFINITY;
}else if(this.minHeap.size() === this.maxHeap.size()){
return (this.minHeap.peek() + this.maxHeap.peek()) / 2;
}else if(this.minHeap.size() > this.maxHeap.size()){
return this.minHeap.peek();
}else{
return this.maxHeap.peek();
}
}
}
const medianheap = new MedianHeap();
medianheap.add(12);
console.log(medianheap.median()) // 12
medianheap.add(2);
console.log(medianheap.median()) // 7
medianheap.add(23);
console.log(medianheap.median()) // 12
medianheap.add(13);
console.log(medianheap.median()) // 12.5
medianheap.add(6);
console.log(medianheap.median())// 12
배열에서 K번째로 작은 수 찾기 / 배열에서 K번째로 큰 수 찾기
주어진 배열을 힙에다가 다 넣고 k번만큼 항목을 꺼내면 된다.
(작은 수를 찾을 땐 최소힙을 이용, 큰 수를 찾을 때는 최대힙을 이용)
🌟🌟🌟 시간 복잡도 O(KlogN) - 항목을 꺼낼때마다 O(logN)이 걸리고, 그걸 k번 반복하니까)
//k번째로 작은 수 찾기
function findKthSmallestNumber(array, k){
const minheap = new MinHeap();
let answer;
for(let i = 0; i < array.length; i++){
minheap.add(array[i]);
}
for(let i = 1; i <= k; i++){
answer = minheap.poll();
}
return answer;
}
const array = [12, 3, 13, 4, 2, 40, 23] // 정렬하면 2, 3, 4, 12, 13, 23, 40
console.log(findKthSmallestNumber(array, 1)); // 2
console.log(findKthSmallestNumber(array, 3)); // 4
console.log(findKthSmallestNumber(array, 6)); // 23
//k번째로 큰 수 찾기
function findKthBiggestNumber(array, k){
const maxheap = new MaxHeap();
let answer;
for(let i = 0; i < array.length; i++){
maxheap.add(array[i]);
}
for(let i = 1; i <= k; i++){
answer = maxheap.poll();
}
return answer;
}
const array2 = [1,6,10,20,90,4]; // 정렬하면 90 20 10 6 4 1
console.log(findKthBiggestNumber(array2, 1)); // 90
console.log(findKthBiggestNumber(array2, 3)); // 10
console.log(findKthBiggestNumber(array2, 6)); // 1
728x90
반응형
'Front-end > 자료구조' 카테고리의 다른 글
| [자료구조] 그래프 (자바스크립트/javascript) (0) | 2021.05.18 |
|---|---|
| [자바스크립트 자료구조] 힙(Heap) - 힙 정렬 / 힙 시간복잡도 (0) | 2021.03.25 |
| [자바스크립트 자료구조] 힙(Heap) - (1) 최소힙, 최대힙 구현 (0) | 2021.03.24 |
| [자료구조] 이진탐색트리 구현 - 삭제 (0) | 2021.03.17 |
| [자료구조] 이진탐색트리 구현 - 최솟값, 최댓값 찾기 / 특정 값 찾기 (0) | 2021.03.17 |