[백준] 1003. 피보나치 함수 (자바스크립트/javascript/js/동적계획법/다이나믹프로그래밍/동적프로그래밍)
2021. 7. 1. 13:16ㆍFront-end/알고리즘
728x90
반응형

문제를 풀기 위한 아이디어
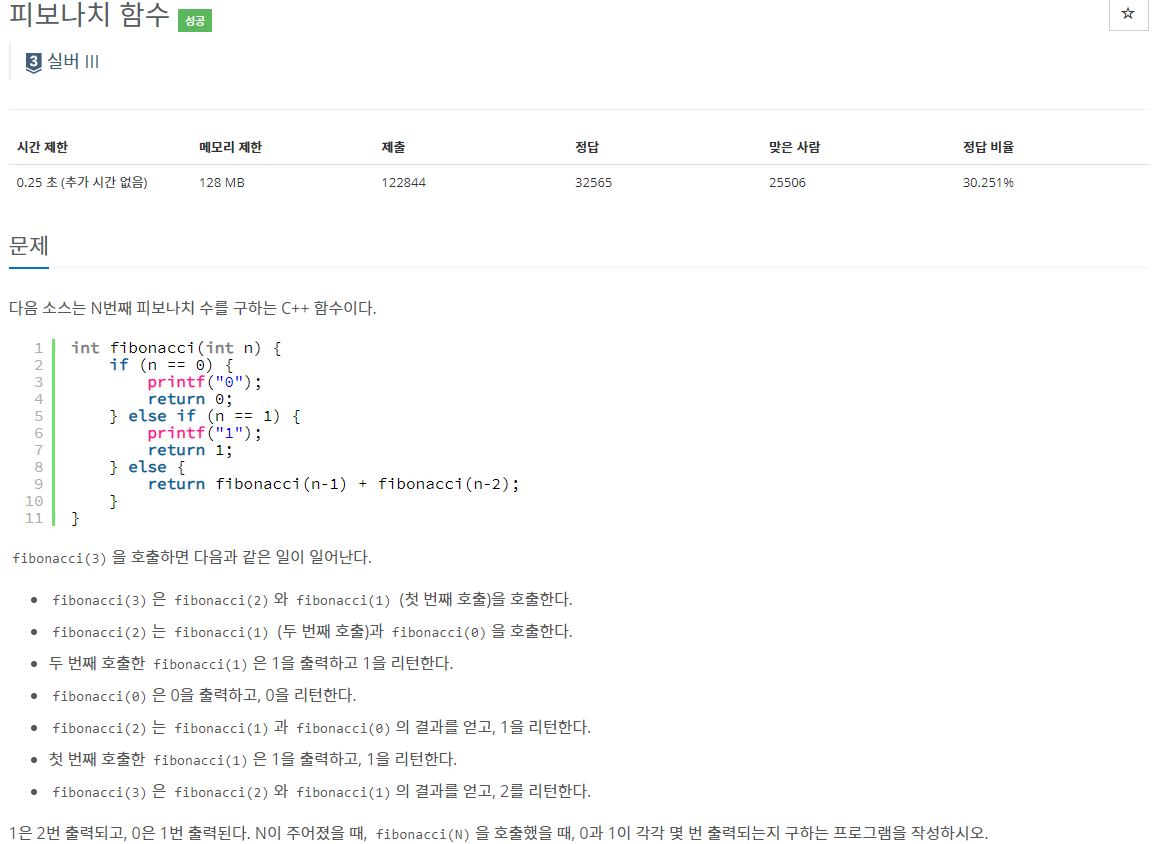
피보나치 수열의 n번째 숫자는 n-2번째 수와 n-1번째 수의 합이 된다.
피보나치 수열을 재귀함수로만 풀 수도 있지만, 이렇게 하게 되면 비교적 작은 수더라도 실행횟수가 어마어마해진다. 예를 들어 fibonacci(5) 함수를 통해 피보나치 수열의 5번째 수를 구하려고 한다면, 아래의 그림과 같다.

fibonacci(5) = fibonacci(4) + fibonacci(3) 이기 때문에, fibonacci(4)는 또 재귀를 부르고 fibonacci(3)도 재귀를 부른다.
이렇게 하면 안좋은 점이 2같은 경우에 3번이나 중복되고 있어 연산회수가 불필요하게 많아지고 있다.
5여서 망정이지 50번째 수만 되더라도 재귀를 쓰면 반복횟수는 어마어마해진다.
따라서 이미 구해놓은 값은 저장해놓고, 그 값을 불러다 쓰기만 하도록 하는 방법을 쓰면 훨씬 간단하게 O(n)의 시간복잡도로 구할 수 있다.
이 문제는 단순한 피보나치 수열을 구하는 문제는 아니고, 피보나치0과 피보나치1이 몇번이나 소환되었는지를 누적해서 구하면 된다. 즉, 피보나치 수열 대신에 피보나치0과 피보나치1이 몇번 소환되었는지만 구한다.
먼저 memo라는 배열을 만들어서 그 안에 입력 최대범위인 40개의 배열을 만들어 0,0으로 채운다.
memo 배열의 각 원소의 [0]과 [1]에는 n번째 수의 피보나치0과 피보나치1의 소환된 횟수가 담길 것이다.
내가 작성한 코드 (자바스크립트)
let fs = require("fs");
let input = fs
.readFileSync("예제.txt")
.toString()
.split("\n")
.map((element) => Number(element));
const N = input[0];
input.shift();
const fibonacci = (number, memo) => {
if (number === 0) {
memo[number] = [1, 0];
return memo[number];
}
if (number === 1) {
memo[number] = [0, 1];
return memo[number];
}
if (number === 2) {
memo[number] = [1, 1];
return memo[number];
}
if (memo[number][0] !== 0 && memo[number][1] !== 0) {
return memo[number];
}
let n_1 = fibonacci(number - 1, memo);
let n_2 = fibonacci(number - 2, memo);
return (memo[number] = [n_1[0] + n_2[0], n_1[1] + n_2[1]]);
};
const memo = Array.from(Array(41), () => new Array(2).fill(0));
for (let i = 0; i < N; i++) {
console.log(fibonacci(input[i], memo).join(" "));
}
728x90
반응형
'Front-end > 알고리즘' 카테고리의 다른 글
| [알고리즘] 동적계획법 (동적프로그래밍, 다이나믹 프로그래밍) (자바스크립트/javascript/js) (0) | 2021.07.01 |
|---|---|
| [백준] 1904. 01타일 (자바스크립트/javascript/js/동적계획법/다이나믹프로그래밍/동적프로그래밍) (0) | 2021.07.01 |
| [백준] 2960. 에라토스테네스의 체 (자바스크립트/javascript/js) (0) | 2021.07.01 |
| [프로그래머스] 디스크 컨트롤러 (자바스크립트/js/javascript/우선순위큐/힙) (0) | 2021.06.30 |
| [프로그래머스] 여행경로 (자바스크립트/javascript/js) (0) | 2021.06.28 |